Modelos para determinar la radiación de calor en grandes incendios de líquidos combustibles y gases
 Los
incendios industriales pueden ser intensos emisores de calor, humo, y
otros productos de la combustión. Esto es comprensible si sabemos que
la sustancia más usada como combustible tiene como base el petróleo el
cual tiene un alto calor de combustión y potencial para generar hollín.
El flujo de energía radiante puede ser lo suficientemente alto como
para poner en peligro la integridad de los edificios circundantes, y la
integridad física de los bomberos, personal de planta y potencialmente
a las personas más allá de los límites de la instalación.
Los
incendios industriales pueden ser intensos emisores de calor, humo, y
otros productos de la combustión. Esto es comprensible si sabemos que
la sustancia más usada como combustible tiene como base el petróleo el
cual tiene un alto calor de combustión y potencial para generar hollín.
El flujo de energía radiante puede ser lo suficientemente alto como
para poner en peligro la integridad de los edificios circundantes, y la
integridad física de los bomberos, personal de planta y potencialmente
a las personas más allá de los límites de la instalación.
El
Departamento de Vivienda y Desarrollo Urbano de los EEUU ha establecido
como límite máximo de radiación térmica un flujo de 31.5 kW/ para estructuras y 1.4 kW/
para estructuras y 1.4 kW/ para
personas como los parámetros para determinar cuál sería una Distancia
de Separación Aceptable (DSA) entre un incendio que de líquidos o gases
y las estructuras y las personas cercanas.
para
personas como los parámetros para determinar cuál sería una Distancia
de Separación Aceptable (DSA) entre un incendio que de líquidos o gases
y las estructuras y las personas cercanas.
Entendamos que 1 kW/ es aproximadamente la
radiación solar recibida en un día de verano.
es aproximadamente la
radiación solar recibida en un día de verano.
Entendamos que 1 kW/
Además
de los parámetros establecidos por el gobierno de los EEUU podemos
también tomar otras referencias de resistencia a la radiación, por
ejemplo la NTP 326: Radiación térmica en incendios de líquidos y gases,
de España nos da como valores de referencia para máxima radiación
tolerable:
Materiales
Pared de ladrillos 400 kW /
Hormigón armado 200 kW /
Cemento 60 kW /
Acero 40 kW /
Madera 10 kW /
Personas
Personas solo durante 20 segundos 6.5 kW /
Bomberos y personas con ropa protectora 4.7 kW /
Personas desprotegidas 4.0 kW /
Antes
de revisar con detalle los procesos de predicción, debemos entender que
los valores obtenidos en algunos casos pueden resultar en un flujo de
radiación mayor a las que realmente pueden obtenerse en experimentos
reales de campo. El origen de esta sobredimensión está basado en que
los cálculos asumen que la superficie en combustión está totalmente
despejada de humo, lo cual no es cierto. En la mayoría de grandes
incendios se generan considerables cantidades de humo dependiendo de la
cantidad de combustible y el tamaño del fuego, al punto que hasta un
20% de la masa del combustible se convierte en partículas en suspensión derivadas
del proceso de combustión incompleta. Este humo resultante se convierte
en una barrera y genera cierta resistencia para la radiación del calor.
Este efecto se vuelve más notable en fuegos a grandes escalas (decenas
de metros de diámetro) ya que en estas condiciones la eficiencia del
combustible disminuye considerablemente.
Figura 1
Desarrollo teórico
El objetivo de este análisis es llegar a una
metodología para
estimar el flujo de radiación térmica en incendios grandes en
combustibles líquidos y gases. En este caso vamos a tomar valores de
los combustibles más comunes como Diesel, petróleo crudo, gasolina,
combustible para aviones, keroseno y tolueno. Algunos de los gases
incluidos en las tablas de esta investigación son el butano, hidrógeno,
GNL, GLP y propano. El análisis de incendios en líquidos inflamables o
combustibles es relativamente independiente del tipo de líquido; el
Poder Calorífico (kJ/kg) y el potencial para liberación de calor
radiante (kW / ) no
varían significativamente de combustible a combustible, ni tampoco la
naturaleza de los incendios.
) no
varían significativamente de combustible a combustible, ni tampoco la
naturaleza de los incendios.
Por otro lado, los gases inflamables almacenados bajo presión, en especial el GLP y el GNL no son aún modelables matemáticamente. Hay una serie de referencias de incendios en GLP y GNL en la que las nubes de gas se encendieron formando bolas de fuego que han llegado incluso a cientos de metros de diámetro. La radiación térmica de los incendios de gases en tanques de almacenamiento puede llegar a provocar un B.L.E.V.E. lo cual no sólo produce una enorme cantidad de radiación térmica, sino también, a menudo, hace que las partes del tanque sean lanzadas a decenas o cientos de metros de distancia.
Por otro lado, los gases inflamables almacenados bajo presión, en especial el GLP y el GNL no son aún modelables matemáticamente. Hay una serie de referencias de incendios en GLP y GNL en la que las nubes de gas se encendieron formando bolas de fuego que han llegado incluso a cientos de metros de diámetro. La radiación térmica de los incendios de gases en tanques de almacenamiento puede llegar a provocar un B.L.E.V.E. lo cual no sólo produce una enorme cantidad de radiación térmica, sino también, a menudo, hace que las partes del tanque sean lanzadas a decenas o cientos de metros de distancia.
En
particular, el GLP es tan volátil que es más probable que se vaporice
antes de formar un depósito de líquido, por lo tanto muchos de los
parámetros de esta investigación en grandes incendios de combustible en
fase líquida no puede ser aplicable a los incendios de GLP. La
predicción del flujo de radiación térmica de un incendio en una fuga de
gases combustibles es mucho más complicada que la de un fuego de
combustible líquido debido a que hay un número de escenarios
potenciales que deben ser tomados en cuenta. En un incendio de
combustible líquido, la dinámica del fuego ha sido mucho más conocida y
estudiada que con en combustible gaseosos.
En
lugar de desarrollar una metodología separada para la estimación del
flujo de radiación térmica para cada escenario de incendio en gases, es
preferible emplear un procedimiento simple que abarca una gran variedad
de escenarios, esta metodología elimina la mayor parte de los
parámetros geométricos del cálculo, pero que sigue siendo lo bastante
conservadora con un margen razonable de seguridad. Este método se
conoce como modelo de "fuente puntual" de radiación. Todo lo que
requiere es estimar la tasa de liberación de calor total del incendio,
y la fracción de esa energía que se emite en forma de radiación
térmica. Esta información está disponible gracias a mediciones de campo
por medio de radiómetros.
El método de "fuente puntual" es preciso en
modelos de que simulan incendios de grandes dimensiones, pero se
considera demasiado conservador en incendios pequeños, porque asume que
toda la energía radiante del incendio se emite desde un solo punto en
vez de distribuirse a través de una forma ideal destinada a representar
el fuego en un modelo predictivo (por lo general un cono o cilindro).
En
caso de incendios en combustible líquido el modelo de “fuente puntual”
puede ser demasiado conservador ya que estos incendios son más
predecibles y hay muchos más datos experimentales disponibles para
validar un modelo con más detalles. Un método sencillo y muy usado para
calcular el flujo de radiación de los grandes incendios de líquido
contenido es el método de "llama sólida". En este caso el fuego es
idealizado como un sólido vertical (un cilindro) y la radiación térmica
es emitida por los lados del cilindro. Este modelo es relativamente
simple, pero requiere calcular el diámetro y la altura del “cilindro”,
así como realizar una estimación de la potencia de emisión.
El
método para determinar la altura de la llama y el ancho del incendio
que formarán el cilindro idealizado serán mostrados más adelante en la
siguiente sección.
Figura 3
Modelado en líquidos combustibles
En el modelo de la radiación de “llama
sólida”, el flujo de radiación térmica, 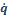 ´´, de un incendio a un objeto cercano está dado
por la expresión:
´´, de un incendio a un objeto cercano está dado
por la expresión:
Donde:
Para fuegos apenas mayores de unos pocos
metros de diámetro, la emisividad efectiva de la llama (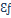 ) puede ser tomada como
valor 1. Además, para estar en el lado conservador, la transmisividad (
) puede ser tomada como
valor 1. Además, para estar en el lado conservador, la transmisividad (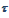 ) se tomará también como uno. De este modo lo
que queda por modelar son el factor de visibilidad (
) se tomará también como uno. De este modo lo
que queda por modelar son el factor de visibilidad (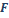 ) y la potencia de emisión total de la llama (
) y la potencia de emisión total de la llama (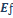 ).
).
La
medición de la potencia de emisión de grandes incendios es difícil y
está sujeta a una gran incertidumbre. Los métodos de cálculo en el
pasado, incluidas las directrices de 1975 HUD (Department of Housing and Urban
Development de los EE.UU.) , consideraban el factor de
visibilidad y
la potencia de emisión de forma independiente, lo que en algunos
escenarios de incendio condujo a predicciones excesivas de la emisión
de radiación total de energía total del incendio. La deficiencia de
estos análisis fue la falta de una estimación global de toda la
energía. Este problema se ha corregido en las últimas décadas, ya que
ahora se usa un parámetro muy bien reconocido por el campo de la
ingeniería de protección contra incendios que es la “tasa de liberación
de calor total de un incendio” (HRR por sus siglas en inglés para Heat
Release Rate) la cual es la mejor medida del potencial para que la
energía radiante pueda causar daño.
Por
otra parte, el HRR en un incendio es mucho más fácil de estimar que la
temperatura o tamaño físico debido a que el HRR es proporcional a la tasa
de consumo de combustible, una cantidad que es relativamente fácil de
medir. El NIST ha realizado cerca de cien experimentos de incendios a
gran escala en las últimas dos décadas, con una variedad de
combustibles líquidos y gases, y una ha demostrado que un de las
medidas más confiables es el de la velocidad de combustión de masa, de
la cual se estima el HRR. Una fracción del HRR total del fuego se emite
en forma de radiación térmica. Para incendios de hasta aproximadamente
cuatro metros de diámetro, la relación entre la tasa de energía radiada
a los alrededores con respecto la
HRR total del incendio, (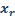 ),
es entre 0.30 y 0.40, y este valor disminuye con el aumento del
diámetro del incendio debido al oscurecimiento del humo. Gran parte de
la radiación térmica de un gran incendio que genera humo y hollín es
emitido por la "pared" de la llama luminosa y visible que rodea la base
del fuego.
),
es entre 0.30 y 0.40, y este valor disminuye con el aumento del
diámetro del incendio debido al oscurecimiento del humo. Gran parte de
la radiación térmica de un gran incendio que genera humo y hollín es
emitido por la "pared" de la llama luminosa y visible que rodea la base
del fuego.
Figura 4
Las
llamas por encima de esta pared luminosa suelen estar ocultas a la
vista por el humo formado debido a la combustión incompleta. El aire es
absorbido desde la
base del fuego y en el proceso de combustión el humo se forma
rápidamente en las partes altas, creando una barrera térmica que se
eleva sobre el fuego y que atrapa gran parte de la energía radiante que
es emitida desde el interior del incendio.
Una
imagen idealizada de incendio utilizado en la mayoría de los modelos
para cálculo de radiación térmica es una en la que el fuego toma una
forma cilíndrica con una altura H y
un diámetro D con
una HRR total de 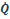 . La mayoría de veces el incendio tendrá una
forma arbitraria pero con una longitud de perímetro P. Con estos parámetros podemos expresar la
energía radiante del siguiente modo:
. La mayoría de veces el incendio tendrá una
forma arbitraria pero con una longitud de perímetro P. Con estos parámetros podemos expresar la
energía radiante del siguiente modo:
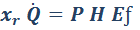 (Ecuación 2)
(Ecuación 2)En mediciones hechas con radiómetro sobre experimentos de incendios a gran escala han demostrado que el
(Donde 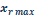 = 0.35 y k = 0.05
= 0.35 y k = 0.05 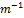 )
)
Curva 1
La fracción de radiación (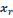 ) es una función del diámetro del fuego D para
Heptano (*), Crudo (°) y kerosene (+).
) es una función del diámetro del fuego D para
Heptano (*), Crudo (°) y kerosene (+).
La línea sólida es la curva que se acerca más
a las dispersiones cuando 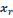 =
= 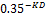 donde k = 0.05 (Ver Ecuación 3).
donde k = 0.05 (Ver Ecuación 3).
Estos
valores se basan en un ajuste de la curva a los datos experimentales
donde se probaron una serie de diferentes líquidos combustibles. El
total de la HRR del incendio (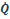 ) se puede expresar también como el producto
de la velocidad de liberación de calor por unidad de área (
) se puede expresar también como el producto
de la velocidad de liberación de calor por unidad de área ( 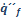 ) por el área (A) de la base del fuego.
) por el área (A) de la base del fuego.
Para un combustible dado, la velocidad de
liberación de calor por unidad de área ( 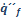 )
es relativamente constante debido a la velocidad de combustión de la
masa de combustible por unidad de área es relativamente constante. El
HRR está medido en kW /
)
es relativamente constante debido a la velocidad de combustión de la
masa de combustible por unidad de área es relativamente constante. El
HRR está medido en kW / , las tablas con los HRR por unidad de área (
, las tablas con los HRR por unidad de área ( 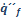 ) de los combustibles más usados las
mostraremos más adelante.
) de los combustibles más usados las
mostraremos más adelante.
Los dos parámetros restantes de la Ecuación 2
son 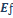 (Potencia de Emisión) y H (la
altura del cilindro idealizado). Los valores reportados de
(Potencia de Emisión) y H (la
altura del cilindro idealizado). Los valores reportados de 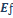 para
líquidos y gases inflamables varían mucho de una fuente a otra. La
variación en los valores reportados de potencia de emisión tiene que
ver con la definición de la altura del cilindro idealizado que
representa el incendio. Un incendio real presenta una considerable
cantidad de humo cuando es visto desde la distancia, con ocasionales
estallidos de llama luminosa en las zonas altas dentro de la masa del
humo.
para
líquidos y gases inflamables varían mucho de una fuente a otra. La
variación en los valores reportados de potencia de emisión tiene que
ver con la definición de la altura del cilindro idealizado que
representa el incendio. Un incendio real presenta una considerable
cantidad de humo cuando es visto desde la distancia, con ocasionales
estallidos de llama luminosa en las zonas altas dentro de la masa del
humo.
La
altura de la llama en un incendio real se define como la extensión
vertical de la región de combustión, y que puede ser expresada como la
altura máxima por encima del suelo en el que estos estallidos de llama
luminosa se pueden ver (ver figura 1).
Tomando
un fuego como una forma cilíndrica idealizada con una altura igual a la
altura de la llama del fuego real (Ver figura 3), en promedio solo
cerca del 20% del área de la superficie del cilindro idealizado consta
de llamas visibles y el 80% restante es humo (ver figura 4). La mayor
parte de la llama es visible está en la base del fuego, aunque
periódicamente algunos estallidos de llama luminosa pueden irrumpir a
través de la columna de humo en las partes altas.
Debemos tener en cuenta que los valores
reportados para 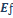 son
a menudo valores promedio para toda la altura de la llama dentro del
cilindro, por lo tanto la Potencia de Emisión de la parte luminosa en
la base del incendio será significativamente menor. Si la relativamente
baja Potencia de Emisión promedio
se aplica a toda la superficie del cilindro idealizado cuya altura H es
igual a la altura de la llamas en un incendio real ubicado a distancias
mayores unas pocas veces el diámetro del incendio, entonces la
estimación del flujo de radiación será exacta. Sin embargo, en
distancias más cercanas las estimaciones de flujo de radiación serán
subestimadas debido a que se asume que la energía radiante será
distribuida por toda la altura del fuego, en lugar de concentrarla
cerca de la base donde se encuentra la masa de combustible como sucede
en la realidad. (Ver figura 3).
son
a menudo valores promedio para toda la altura de la llama dentro del
cilindro, por lo tanto la Potencia de Emisión de la parte luminosa en
la base del incendio será significativamente menor. Si la relativamente
baja Potencia de Emisión promedio
se aplica a toda la superficie del cilindro idealizado cuya altura H es
igual a la altura de la llamas en un incendio real ubicado a distancias
mayores unas pocas veces el diámetro del incendio, entonces la
estimación del flujo de radiación será exacta. Sin embargo, en
distancias más cercanas las estimaciones de flujo de radiación serán
subestimadas debido a que se asume que la energía radiante será
distribuida por toda la altura del fuego, en lugar de concentrarla
cerca de la base donde se encuentra la masa de combustible como sucede
en la realidad. (Ver figura 3).
Por ejemplo, para los incendios de más de 30 m de
diámetro, la potencia de emisión promedio reportada por muchos
investigadores es de menos de 31,5 kW / ,
el valor de umbral utilizado por la HUD para determinar la Distancia de
Separación Aceptable (ASD por sus siglas en inglés) para los edificios
y estructuras combustibles. Las curvas 2-3-4 muestran correlaciones
empíricas de potencia de emisión,
,
el valor de umbral utilizado por la HUD para determinar la Distancia de
Separación Aceptable (ASD por sus siglas en inglés) para los edificios
y estructuras combustibles. Las curvas 2-3-4 muestran correlaciones
empíricas de potencia de emisión, 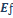 y altura de la llama H para
dos de los métodos más ampliamente utilizados para predecir la
radiación térmica en grandes incendios en comparación con la
correlación desarrollada en esta investigación.
y altura de la llama H para
dos de los métodos más ampliamente utilizados para predecir la
radiación térmica en grandes incendios en comparación con la
correlación desarrollada en esta investigación.
Tanto el método de Shokri
y Beyler y el método de Mudan y
Croce utilizan una potencia de
emisión promedio sobre
la altura de la llama del fuego. Ambas correlaciones caen por debajo de
31,5 kW / en
incendios superiores a 30 m de diámetro (ver Curva 2). Estas
correlaciones pueden interpretarse erróneamente en el sentido de que
los edificios se pueden construir junto a los lugares donde pueden
darse incendios potencialmente grandes, simplemente porque el flujo
predicho nunca superaría
los 31,5 kW /
en
incendios superiores a 30 m de diámetro (ver Curva 2). Estas
correlaciones pueden interpretarse erróneamente en el sentido de que
los edificios se pueden construir junto a los lugares donde pueden
darse incendios potencialmente grandes, simplemente porque el flujo
predicho nunca superaría
los 31,5 kW / independientemente
de la distancia del fuego. Debido a que las pautas de la HUD tienen que
tomar en cuenta tanto instalaciones cercanas como lejanas al punto del
incendio, y debido a la importancia de la evaluación de la eficacia de
las barreras térmicas, la metodología para la predicción de flujo de
radiación térmica tiene que ser aplicable en todo el rango de tamaños
de incendios y a todas las distancias de separación.
independientemente
de la distancia del fuego. Debido a que las pautas de la HUD tienen que
tomar en cuenta tanto instalaciones cercanas como lejanas al punto del
incendio, y debido a la importancia de la evaluación de la eficacia de
las barreras térmicas, la metodología para la predicción de flujo de
radiación térmica tiene que ser aplicable en todo el rango de tamaños
de incendios y a todas las distancias de separación.
La metodología adoptada aquí produce más o menos el mismo producto
Por motivos de simplicidad, aquí hemos
adoptado una constante Potencia de Emisión de 100 kW / ,
ya que ha sido citado en varias investigaciones como la potencia de
emisión de los puntos luminosos de incendios en gasolina y querosene.
La altura de la zona de llama luminosa, H,
se puede encontrar por medio de la Ecuación2. Para simplificar el
análisis, se supone siempre que el área del incendio es circular donde
,
ya que ha sido citado en varias investigaciones como la potencia de
emisión de los puntos luminosos de incendios en gasolina y querosene.
La altura de la zona de llama luminosa, H,
se puede encontrar por medio de la Ecuación2. Para simplificar el
análisis, se supone siempre que el área del incendio es circular donde
P = π D y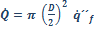 ,
,
pero esto no es una suposición restrictiva, ya que un incendio en líquidos puede tomar formas arbitrarias.
P = π D y
pero esto no es una suposición restrictiva, ya que un incendio en líquidos puede tomar formas arbitrarias.
Sustituyendo las expresiones de 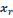 y
y 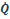 en la Ecuación 2 podemos inferir una
expresión válida para la altura de H:
en la Ecuación 2 podemos inferir una
expresión válida para la altura de H:
H = 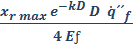 (Ecuación 5)
(Ecuación 5)
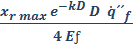 (Ecuación 5)
(Ecuación 5)
Curva 2
Poder de Emisión 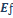 expresado en kW /
expresado en kW / como una función del
diámetro del incendio para una poza de gasolina prendida.
como una función del
diámetro del incendio para una poza de gasolina prendida.
Curva 3
Altura de la llama como una función del
diámetro del incendio para una poza de gasolina prendida.
Escenarios de incendio con diámetros mayores
a 20 metros H se
representa como una función de D en
la Curva 5. En dicha curva H alcanza
su máximo valor cuando D =
20 m.
Debido a la escasez de datos sobre la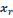 y
y 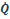 para incendios muy
grandes, se supone que para los incendios con diámetros superiores a 20 m, la altura de la zona de la llama luminosa
se mantiene en su máximo valor.
para incendios muy
grandes, se supone que para los incendios con diámetros superiores a 20 m, la altura de la zona de la llama luminosa
se mantiene en su máximo valor.
Debido a la escasez de datos sobre la
El valor máximo de H se encuentra mediante la sustitución de D = 20 m,
donde 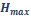 resulta como una magnitud medida en m y
resulta como una magnitud medida en m y 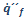 como una magnitud medida en kW /
como una magnitud medida en kW / . La mayoría de los cálculos de riesgo de
incendios potenciales incluyen escenarios mayores que 20 m de
diámetro. En estos casos, lo único que se requiere para obtener la
altura de la zona luminosa es una estimación de la tasa de liberación
de calor por unidad de área.
. La mayoría de los cálculos de riesgo de
incendios potenciales incluyen escenarios mayores que 20 m de
diámetro. En estos casos, lo único que se requiere para obtener la
altura de la zona luminosa es una estimación de la tasa de liberación
de calor por unidad de área.
La Curva 4 compara el producto de 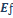 y H para
las tres metodologías. En caso de incendios cuya diámetros figuran
entre 1 m y
50 m, los tres métodos arrojan valores similares
de
y H para
las tres metodologías. En caso de incendios cuya diámetros figuran
entre 1 m y
50 m, los tres métodos arrojan valores similares
de 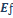 * H con la metodología
usada en este documento los resultados serán más conservadores. En un
incendio que tiene más de 50 m de
diámetro, los métodos difieren debido a que los modelos y sus
experimentos de campo en los que se basan las correlaciones no incluían
ningún incendio con estas medidas. Las pautas de la HUD, sin embargo,
deben tener en cuenta los incendios cuyos diámetros potencialmente
pueden llegar a cientos de metros. La presente metodología asume que
más allá de alrededor de 20 m, el flujo de energía radiante por unidad de
longitud del perímetro del incendio,(
* H con la metodología
usada en este documento los resultados serán más conservadores. En un
incendio que tiene más de 50 m de
diámetro, los métodos difieren debido a que los modelos y sus
experimentos de campo en los que se basan las correlaciones no incluían
ningún incendio con estas medidas. Las pautas de la HUD, sin embargo,
deben tener en cuenta los incendios cuyos diámetros potencialmente
pueden llegar a cientos de metros. La presente metodología asume que
más allá de alrededor de 20 m, el flujo de energía radiante por unidad de
longitud del perímetro del incendio,(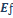 * H ),
sigue siendo relativamente constante, lo que permite predicciones del
flujo de radiación de muy grandes incendios que nunca han sido
estudiado experimentalmente.
* H ),
sigue siendo relativamente constante, lo que permite predicciones del
flujo de radiación de muy grandes incendios que nunca han sido
estudiado experimentalmente.
Curva 4
Flujo de energía radiante (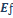 * H) como una función del diámetro del incendio
para una poza de gasolina prendida.
* H) como una función del diámetro del incendio
para una poza de gasolina prendida.
Lo
que queda por calcular para flujo de radiación térmica utilizando la
Ecuación 1 es la determinación del Factor de Visibilidad (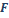 )
del fuego hacia un objetivo.
)
del fuego hacia un objetivo.
El cálculo del factor de visibilidad se puede simplificar suponiendo que el fuego está rodeado por una pared vertical de altura H que emite una energía radiante a una velocidad de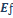 ,
y que dicha pared se compone de elementos circulares o lineales para
los que existen tablas analíticas para determinar el factor de
visibilidad.
,
y que dicha pared se compone de elementos circulares o lineales para
los que existen tablas analíticas para determinar el factor de
visibilidad.
El cálculo del factor de visibilidad se puede simplificar suponiendo que el fuego está rodeado por una pared vertical de altura H que emite una energía radiante a una velocidad de
Curva 5
La altura de la zona de llama luminosa para
un incendio de gasolina, donde 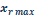 = 0.35, k = 0.05
= 0.35, k = 0.05 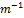 ,
, 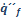 =2400 kW /
=2400 kW / y
y 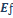 = 100 kW /
= 100 kW / .
(Ver la Ecuación 5). En general la máxima altura de la llama en la zona
luminosa de un incendio en una poza de líquido combustible será dada por
.
(Ver la Ecuación 5). En general la máxima altura de la llama en la zona
luminosa de un incendio en una poza de líquido combustible será dada por 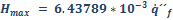 , donde
, donde 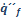 es el HRR por unidad de área expresado en kW /
es el HRR por unidad de área expresado en kW / . La línea punteada en la gráfica indica
. La línea punteada en la gráfica indica 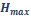
Cálculo de Barreras Térmicas
La presencia de las barreras térmicas hechas
por el hombre o de barreras naturales pueden ser
incorporadas en el cálculo del factor de visibilidad. Aunque la
metodología presentada en esta sección está diseñada para ser
conservadora, sus resultados con respecto al uso de barreras no
necesariamente lo son. Debido a que la emisión de energía radiante se
concentra cerca de la base del fuego en lugar de estar distribuido a lo
largo de toda la altura del fuego y humo, la eficacia de una barrera
térmica como bloqueo de la radiación térmica puede resultar
sobre dimensionada.
Mediciones recientes en Japón en incendios de
crudo de 20 m de
diámetro mostraron que el 85% de la energía radiante del fuego fue
emitida en alturas inferiores a 20 m.
El 15% restante de la energía radiante es emitida por el humo negro
caliente en los niveles superiores, y por destellos luminosos
ocasionales de llama. La HRR por unidad de área (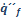 ) para el crudo es de aproximadamente 2000 kW /
) para el crudo es de aproximadamente 2000 kW / , por lo tanto de acuerdo a la Ecuación 6, la
altura de la llama luminosa (
, por lo tanto de acuerdo a la Ecuación 6, la
altura de la llama luminosa (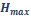 ) para una poza prendida de 20 m de
diámetro fuego diámetro será
) para una poza prendida de 20 m de
diámetro fuego diámetro será 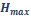 =
= 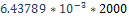 = 12.87 m. En este contexto, se podría esperar que una
barrera térmica de 13 m de
altura pueda bloquear toda la radiación térmica. Para remediar esta
situación, se sugirió que, solo para
efectos de la evaluación de efectividad de barreras térmica, la
Potencia de Emisión en la zona de la llama luminosa (
= 12.87 m. En este contexto, se podría esperar que una
barrera térmica de 13 m de
altura pueda bloquear toda la radiación térmica. Para remediar esta
situación, se sugirió que, solo para
efectos de la evaluación de efectividad de barreras térmica, la
Potencia de Emisión en la zona de la llama luminosa (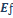 ) sea reducido a la mitad, (de 100 kW/
) sea reducido a la mitad, (de 100 kW/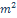 a 50 kW /
a 50 kW /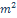 ).
).
La conservación de energía será preservada pero la altura de la zona luminosa en la Ecuación 6 se duplicará como resultado de la estimación más baja de la potencia de emisión. La cantidad resultante de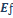 * H sigue siendo la
misma, por lo tanto la predicción de flujo de radiación térmica en
grandes distancias sigue siendo la misma.
* H sigue siendo la
misma, por lo tanto la predicción de flujo de radiación térmica en
grandes distancias sigue siendo la misma.
La conservación de energía será preservada pero la altura de la zona luminosa en la Ecuación 6 se duplicará como resultado de la estimación más baja de la potencia de emisión. La cantidad resultante de
El rango de potencias de emisión de 100 kW/ y 50 kW /
y 50 kW / no
es arbitraria. Muchos investigadores han realizado mediciones de
potencia de emisión sobre grandes incendios en pozas que han caído
dentro de este rango. Es una medición muy difícil de hacer porque, en
realidad, la potencia de emisión es espacial y temporalmente variable.
La elección de 100 kW/
no
es arbitraria. Muchos investigadores han realizado mediciones de
potencia de emisión sobre grandes incendios en pozas que han caído
dentro de este rango. Es una medición muy difícil de hacer porque, en
realidad, la potencia de emisión es espacial y temporalmente variable.
La elección de 100 kW/ para los cálculos de
riesgos en distancias cortas y de 50 kW /
para los cálculos de
riesgos en distancias cortas y de 50 kW / para
la evaluación de las barreras térmicas están destinados a proporcionar
estimaciones conservadoras de las Distancias Aceptables de Separación
(ASD).
para
la evaluación de las barreras térmicas están destinados a proporcionar
estimaciones conservadoras de las Distancias Aceptables de Separación
(ASD).
Tabla 1
Tabla 2
Factor de Visibilidad 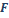 en un incendio de
forma idealizada cilíndrica hacia un punto que recibe la radiación
máxima. Note que H es
la altura del cilindro D es
el diámetro del cilindro, S es
la distancia desde el borde del incendio hasta el punto que recibe la
radicación. Se
asume que el elemento que recibe la radiación tiene la misma altura que
la base del cilindro. (Ver esquema 1)
en un incendio de
forma idealizada cilíndrica hacia un punto que recibe la radiación
máxima. Note que H es
la altura del cilindro D es
el diámetro del cilindro, S es
la distancia desde el borde del incendio hasta el punto que recibe la
radicación. Se
asume que el elemento que recibe la radiación tiene la misma altura que
la base del cilindro. (Ver esquema 1)
Tablas para cálculo de 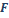 (Plano Vertical)
(Plano Vertical)
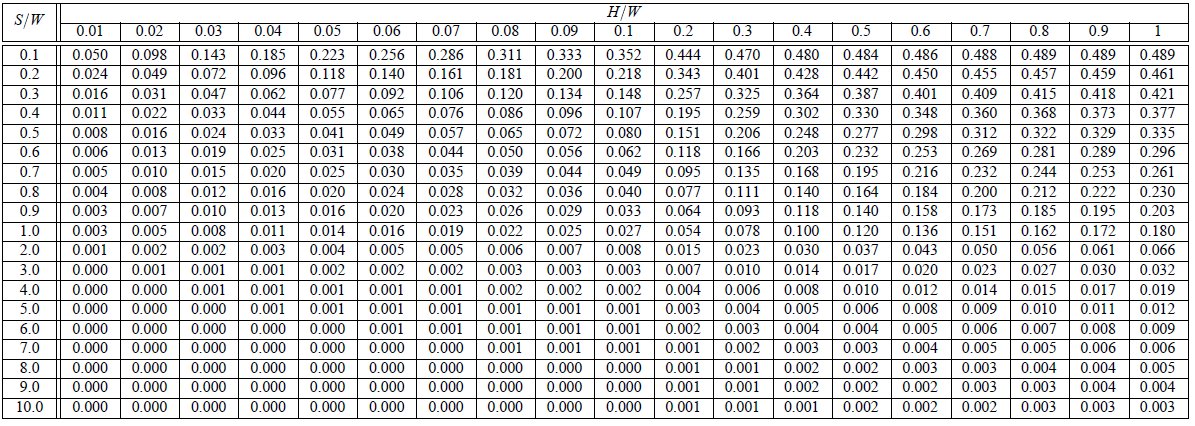
Tabla 3
Factor de Visibilidad 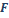 en un incendio de
lineal asumiendo un plano elevado hacia un punto que recibe la
radiación máxima. Note que H es
la altura del plano W es
el ancho del plano, S es
la distancia desde el centro del plano hasta el punto que recibe la
radicación. Se
asume que el elemento que recibe la radiación tiene la misma altura que
la base del plano. (Ver esquema 1)
en un incendio de
lineal asumiendo un plano elevado hacia un punto que recibe la
radiación máxima. Note que H es
la altura del plano W es
el ancho del plano, S es
la distancia desde el centro del plano hasta el punto que recibe la
radicación. Se
asume que el elemento que recibe la radiación tiene la misma altura que
la base del plano. (Ver esquema 1)
El uso de planos verticales es útil para
modelar incendios de gases, donde la distancia S´ es obtenida mediante una ecuación que veremos
más adelante.
Esquema para valores W, S, D
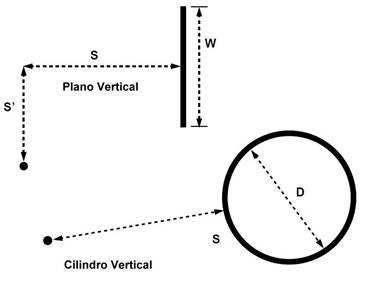
Esquema 1
En la siguiente entrega veremos los modelos que se usan para poder modelar un incendio en gases y compararemos estos modelos con las metodologías similares europeas.
Fuentes:
-NTP 326: Radiación térmica en incendios de líquidos y gases - CENTRO NACIONAL DE CONDICIONES DE TRABAJO
-Termal Radiation from Large Pool Fires Nov 2000 - NIST
-LARGE-SCALE POOL FIRES - BRE Centre for Fire Safety Engineering, The University of Edinburgh
-Large LNG Fire Thermal Radiation – Technology & Management Systems, Inc
Traducción/Recopilación: Martin Palma Camargo - HSE PERÚ - 2013
En la siguiente entrega veremos los modelos que se usan para poder modelar un incendio en gases y compararemos estos modelos con las metodologías similares europeas.
Fuentes:
-NTP 326: Radiación térmica en incendios de líquidos y gases - CENTRO NACIONAL DE CONDICIONES DE TRABAJO
-Termal Radiation from Large Pool Fires Nov 2000 - NIST
-LARGE-SCALE POOL FIRES - BRE Centre for Fire Safety Engineering, The University of Edinburgh
-Large LNG Fire Thermal Radiation – Technology & Management Systems, Inc
Traducción/Recopilación: Martin Palma Camargo - HSE PERÚ - 2013